Rigidity of origami surfaces

El Departamento de Geometría y Topología, junto a la Facultad de Ciencias, tienen el gusto de invitarles a la siguiente conferencia: Rigidity of origami surfaces

Ponente: profesora Ileana Streinu, del Smith College y University of  Massachusetts Amherst (USA).
Fecha: viernes 7 de junio de 2013
Hora: 12.00 horas.
Lugar: Salón de Grados del Edificio Mecenas (patio)

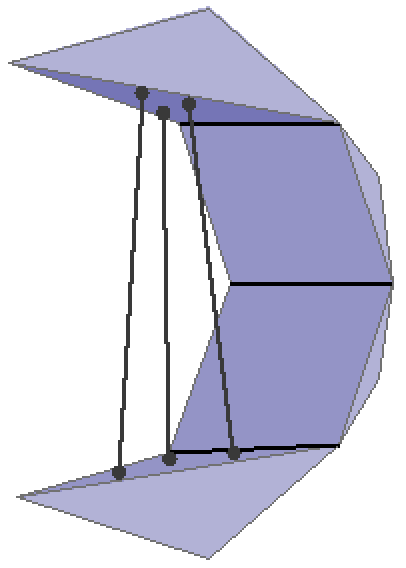
Resumen: Cauchy's famous rigidity theorem for 3D convex polyhedra has been extended in various directions by Dehn, Weyl, A.D.Alexandrov, Gluck and Connelly. These results imply that a disk-like polyhedral surface with simplicial faces is, generically, flexible, if the boundary has at least 4 vertices. What about surfaces with rigid but not necessarily simplicial faces? A natural, albeit extreme family is given by flat-faced origamis. Around 1995, Robert Lang, a well-known origamist, proposed a method for designing a crease pattern on a flat piece of paper such that it has an isometric flat-folded realization with an underlying, predetermined metric tree structure. Important mathematical properties of this algorithm remain elusive to this day. In this talk I will show that Lang's beautiful method leads, most often, to a crease pattern that cannot be continuously deformed to the desired flat-folded shape if its faces are to be kept rigid. Most surprisingly, sometimes the initial crease pattern is simply rigid: the (real) configuration space of such a structure may be disconnected, with one of the components being an isolated point. This is joint work with my PhD student John Bowers, who also implemented a very nice program to visualize what is going on.